본문 바로가기
스터디/알고리즘

[ 알고리즘 ] DFS와 BFS

by 또잉코딩 2021. 1. 4.

DFS(Depth First Search, 깊이 우선 탐색)란?

루트 노드(혹은 다른 임의의 노드)에서 시작해서 다음 분기(branch)로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법으로 스택 또는 재귀 호출을 이용한다.

 

1. 미로를 탐색할 때 한 방향으로 갈 수 있을 때까지 계속 가다가 더 이상 갈 수 없게 되면 다시 가장 가까운 갈림길로 돌아와서 이곳으로부터 다른 방향으로 다시 탐색을 진행하는 방법과 유사함

 

2. 즉 넓게(wide) 탐색하기 전에 깊게(deep) 탐색함

 

3. 모든 노드를 방문하고자 하는 경우에 이 방법을 선택함

 

4. 깊이 우선 탐색(DFS)이 너비 우선 탐색(BFS)보다 좀 더 간단함

 

5. 검색 속도 자체는 너비 우선 탐색(BFS)에 비해서 느림

 

 

DFS의 과정

 

 

DFS의 시간 복잡도

DFS는 그래프(정점의 수 : N, 간선의 수: E)의 모든 간선을 조회함

 

* 인접행렬로 표현된 그래프 : O(N^2)

* 인접 리스트로 표현된 그래프 : O(N+E)

 

 

DFS 구현 코드 - 인접행렬

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.StringTokenizer;

public class Q_1260 {
	static ArrayList<Integer> dfs_result = new ArrayList<Integer>();
	static int[] visited; // 방문 여부 체크
	
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st;
		
		st = new StringTokenizer(br.readLine());
		int N = Integer.parseInt(st.nextToken()); // 정점의 개수
		int M = Integer.parseInt(st.nextToken()); // 간선의 개수
		int V = Integer.parseInt(st.nextToken()); // 탐색을 시작할 정점의 번호
		
		int array[][] = new int[N+1][N+1];
		int x, y;
		for (int i = 0; i < M; i++) {
			st = new StringTokenizer(br.readLine());
			x = Integer.parseInt(st.nextToken());
			y = Integer.parseInt(st.nextToken());
			array[x][y] = array[y][x] = 1;
		}
		
		visited = new int[N+1]; // 방문 초기화
		DFS(array, V);
		
		// 출력
		for (int i = 0; i < dfs_result.size(); i++) {
			System.out.print(dfs_result.get(i) + " ");
		}
	}

	public static void DFS(int[][] arr, int start) {
		visited[start] = 1;
		dfs_result.add(start);

		// 인접 노드 방문했는지 확인
		for (int i = 1; i < arr.length; i++) {
			if (arr[start][i] == 1 && visited[i] == 0)
				DFS(arr, i);
		}
	}
}

DFS 구현 코드 - 인접 리스트

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Collections;
import java.util.StringTokenizer;

public class Q_1260 {
	static ArrayList<Integer> dfs_result = new ArrayList<Integer>();
	static int[] visited; // 방문 여부 체크
	
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st;
		
		st = new StringTokenizer(br.readLine());
		int N = Integer.parseInt(st.nextToken()); // 정점의 개수
		int M = Integer.parseInt(st.nextToken()); // 간선의 개수
		int V = Integer.parseInt(st.nextToken()); // 탐색을 시작할 정점의 번호
		
		ArrayList<ArrayList<Integer>> array = new ArrayList<ArrayList<Integer>>();
		for (int i = 0; i <= N; i++) { // N+1개 생성
			array.add(new ArrayList<Integer>());
		}
		
		int x, y;
		for (int i = 0; i < M; i++) {
			st = new StringTokenizer(br.readLine());
			x = Integer.parseInt(st.nextToken());
			y = Integer.parseInt(st.nextToken());
			array.get(x).add(y);
			array.get(y).add(x);
		}
		
		for (int i = 1; i <= N; i++)
			Collections.sort(array.get(i));
		
		visited = new int[N+1]; // 방문 초기화
		DFS(array, V);
		
		// 출력
		for (int i = 0; i < dfs_result.size(); i++) {
			System.out.print(dfs_result.get(i) + " ");
		}
	}
	
	public static void DFS(ArrayList<ArrayList<Integer>> arr, int start) {
		visited[start] = 1;
		dfs_result.add(start);
		
		// 모든 노드 방문했는지 확인
		for (int i = 0; i < arr.get(start).size(); i++) {
			if (visited[arr.get(start).get(i)] == 0)
				DFS(arr, arr.get(start).get(i));
		}
	}
}

 

 

BFS(Breadth First Search, 너비 우선 탐색)란?

 

루트 노드(혹은 다른 임의의 노드)에서 시작해서 인접한 노드를 먼저 탐색하는 방법으로 큐(선입선출(FIFO) 구조)를 이용한다.

 

1. 시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 순회 방법

 

2. 즉 깊게(deep) 탐색하기 전에 넓게(wide) 탐색하는 것

 

3. 두 노드 사이의 최단 경로 혹은 임의의 경로를 찾고 싶을 때 이 방법을 선택함

 

 

BFS의 과정

 

 

BFS의 시간 복잡도

BFS는 그래프(정점의 수 : N, 간선의 수: E)의 모든 간선을 조회함

 

* 인접행렬로 표현된 그래프 : O(N^2)

* 인접 리스트로 표현된 그래프 : O(N+E)

 

 

BFS 구현 코드 - 인접행렬

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;

public class Q_1260 {
	static ArrayList<Integer> bfs_result = new ArrayList<Integer>();
	static int[] visited; // 방문 여부 체크
	static Queue<Integer> queue = new LinkedList<Integer>();
	
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st;
		
		st = new StringTokenizer(br.readLine());
		int N = Integer.parseInt(st.nextToken()); // 정점의 개수
		int M = Integer.parseInt(st.nextToken()); // 간선의 개수
		int V = Integer.parseInt(st.nextToken()); // 탐색을 시작할 정점의 번호
		
		int array[][] = new int[N+1][N+1];
		int x, y;
		for (int i = 0; i < M; i++) {
			st = new StringTokenizer(br.readLine());
			x = Integer.parseInt(st.nextToken());
			y = Integer.parseInt(st.nextToken());
			array[x][y] = array[y][x] = 1;
		}
		
		visited = new int[N+1]; // 방문 초기화
		BFS(array, V);
		
		// 출력
		for (int i = 0; i < bfs_result.size(); i++) {
			System.out.print(bfs_result.get(i) + " ");
		}
	}
	
	public static void BFS(int[][] arr, int start) {
		visited[start] = 1;
		queue.offer(start);
		
		while(!queue.isEmpty()) {
			int x = queue.poll();
			bfs_result.add(x);
			
			// 모든 노드 방문했는지 확인
			for (int i = 1; i < arr.length; i++) {
				if (arr[x][i] == 1 && visited[i] == 0 && !queue.contains(i)) {
					queue.offer(i);
					visited[i] = 1;
				}
			}
		}
	}
}

BFS 구현 코드 - 인접 리스트

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Collections;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;

public class Q_1260 {
	static ArrayList<Integer> bfs_result = new ArrayList<Integer>();
	static int[] visited; // 방문 여부 체크
	static Queue<Integer> queue = new LinkedList<Integer>();
	
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st;
		
		st = new StringTokenizer(br.readLine());
		int N = Integer.parseInt(st.nextToken()); // 정점의 개수
		int M = Integer.parseInt(st.nextToken()); // 간선의 개수
		int V = Integer.parseInt(st.nextToken()); // 탐색을 시작할 정점의 번호
		
		ArrayList<ArrayList<Integer>> array = new ArrayList<ArrayList<Integer>>();
		for (int i = 0; i <= N; i++) { // N+1개 생성
			array.add(new ArrayList<Integer>());
		}
		
		int x, y;
		for (int i = 0; i < M; i++) {
			st = new StringTokenizer(br.readLine());
			x = Integer.parseInt(st.nextToken());
			y = Integer.parseInt(st.nextToken());
			array.get(x).add(y);
			array.get(y).add(x);
		}
		
		for (int i = 1; i <= N; i++)
			Collections.sort(array.get(i));
		
		visited = new int[N+1]; // 방문 초기화
		BFS(array, V);
		
		// 출력
		for (int i = 0; i < bfs_result.size(); i++) {
			System.out.print(bfs_result.get(i) + " ");
		}
	}
	
	public static void BFS(ArrayList<ArrayList<Integer>> arr, int start) {
		visited[start] = 1;
		queue.offer(start);

		while(!queue.isEmpty()) {
			int x = queue.poll();
			bfs_result.add(x);
			
			// 모든 노드 방문했는지 확인
			for (int i = 0; i < arr.get(x).size(); i++) {
				if (visited[arr.get(x).get(i)] == 0 && !queue.contains(arr.get(x).get(i))) {
					queue.offer(arr.get(x).get(i));
					visited[arr.get(x).get(i)] = 1;
				}
			}
		}
	}
}

 

 

인접행렬로 구현했을 때와 인접 리스트로 구현했을 때의 차이 

왼쪽이 인접행렬, 오른쪽이 인접 리스트 

 

위가 인접행렬, 아래가 인접 리스트로 구현한 코드

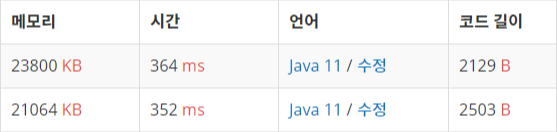
메모리와 시간 측면 모두 인접 리스트가 더 적은 비중을 차지하는 것을 알 수 있다. 

 

 

다음 시간까지 풀어볼 백준 문제

 

 

스터디 일자 : 2021.01.04

스터디 발표자 : 김서영

'스터디 > 알고리즘' 카테고리의 다른 글

[ 알고리즘 ] 다익스트라 알고리즘  (0) 2021.01.31
[ 알고리즘 ] 분할 정복 알고리즘(Divide and conquer algorithm)  (0) 2021.01.18
[ 알고리즘 ] 동적 프로그래밍  (0) 2021.01.11

관련글

티스토리툴바